A Quadtree Based Storage Format and Effective Multiplication Algorithm for Sparse Matrix

Abstract: Sparse matrix multiplication is widely involved in scientific researches and large numbers of applications. However, the traditional storage formats for sparse matrix could introduce a lot of indirect data accessing during the time, which results in high rate of cache misses and poor execution performance. To improve this, we propose a quadtree storage format, derived from recursive divisions of matrix. With this data structure, the original sparse matrix multiplication can be transferred to computations over independent relatively small regions, which can well fit the cache capacity. Therefore, a significant improvement of performance could be achieved. Moreover, this region-based computation framework promises substantial parallelism in distributed computing environment. We elaborate our solution of quadtree-based parallel matrix multiplication, including tuning a better region size, instruction level optimization techniques and computation distribution strategy. Extra cost introduced by this data model is discussed as well. Extensive and comprehensive experiments over real practical matrices shows that the quadtree based sparse matrixvector multiplication has an average of 1.100 speedup of the CSR format, and the sparse matrix-matrix multiplication has an average of 1.862 speedup comparing with the CSR format. The quadtree storage format achieves high performance after employing instruction level optimization techniques, and the experiments in Lenovo Deepcomp7000 demonstrate that the sparse matrix-vector multiplication has an average of 1.63 speedup comparing with the Intel Cluster Math Kernel Library implementation.

Keyword: Sparse matrix; Quadtree; Cache-hit rate; Matrix multiplication algorithm; Distributed parallelism

The recursive decomposition of sparse matrix

The sparse matrix can be recursive decomposed into a number of sub-regions. The region length d effects the matrix storage efficiency (compression ratio) and program execution efficiency significantly. Obviously, in order to improve the Cache data locality, the best case is that data loaded into the cache can complete all of its operations. It cannot be fully achieved, but we can adjust the parameters to approximate the situation. Therefore, an appropriate selection d can help decomposing the matrix into subregions, which is not bigger than the cache. Thus, the entire multiplication divides into independent operations of various sub-regions. It contributes a lot to data locality and the reduction of cache loss.

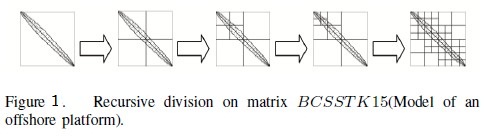
Figure 1 details the process of recursively decomposing a sparse matrix. The process can be expressed as the recursive generation of a quadtree, which is shown in figure 2. This article defines two kinds of intermediate nodes. One is called empty-region (expressed as E), which doesn’t contain nonzero elements and therefore no need to be further decomposed. The other is called mixed-region(expressed as M), which contains nonzero elements and can be decomposed continually. The leaf nodes of a quadtree can also be separated into two kinds: one is empty-region, the other is dense-region (expressed as D which may contain zero elements).

According to the target region length d, the quadtree storage structure has following characteristics: (1) If the size of matrix is n×n,the size of the target region is d×d , then the maximum depth of the tree is Dep=log_dⁿ and the maximum number of intermediate nodes is N = O(4^Dep-1); (2) The overhead to store block information and intermediate node is as follows. During the process of generating the quadtree, each intermediate node contains an index pointer (x, y) to a relate region (occupy a storage space SI ) and the region length d (occupy a storage space SD). The maximum additional space overhead of quadtree is CS = (2SI + SD)×O(4^Dep-1). However, this part of overhead, which is only due to the transformation, organization and representation of the matrix, is not involved in the multiplication process. Therefore, it does not increase the time complexity of computation. (3) Lower Compression ratio comparing with CSR. Since every target region stores nonzero elements in COO format, the total space overhead is CM = nθ(SD+2SI )+CS, where CM is closely related with the matrix sparsity and the size of target region d. In addition, the distribution of nonzero elements will affect the number of leaf nodes too. (4) Elimination of the possible impact of the distribution of nonzero elements in the multiplication. The original multiplication has been divided into independent operations of various sub-regions. Most of these sub-regains have a dense form, based on which the algorithm is more general. (5) Easy to programming. This data structure reflects the process of recursive decomposition. It is suitable for the block matrix multiplication algorithm.

The implementation of Quadtree based storage format

To transform the storage form of a sparse matrix under traditional forms (such as CSR) to quadtree forms, we should take two problems into account. Firstly, traditional tree generation algorithm (such as depth-first algorithm and breadth-first algorithm) are not suitable here, becasue a large number of traverse, search and stack overheads in such algorithms lead to performance reduction. Secondly, The generation process of quadtree should be efficiency.

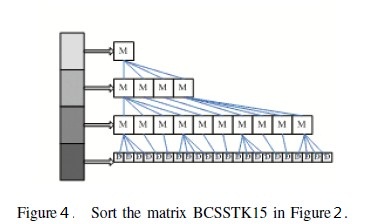
Taking these two problems into account, the designed quadtree structure of a matrix is shown in Figure 3. An original matrix is decomposed into four same-size sub- regions from top to bottom. And then, these 4 sub-regions are decomposed into 4 sub-regions similarly. The decom- position continues until the length of sub-region d is in a given limit d. Then, the matrix are decomposed into leaf nodes successfully. After storing every leaf nodes, the transformation of structure completes. The storage structure in ﬁgure 2 is corresponding to the matrix in ﬁgure 1. Obviously, the computer can index to the leaf node directly. The quadtree structure not only reduces space overhead, but also eliminates the overhead of stack and queue operations.

Performance

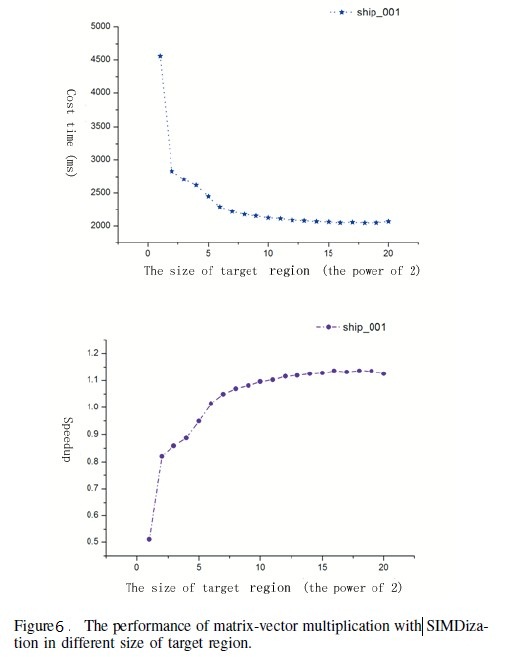
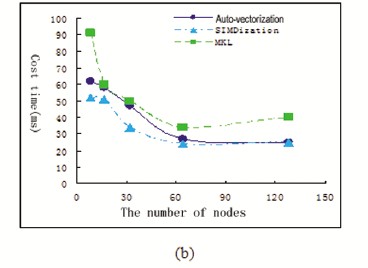
Authors

Ji-Lin Zhang,Department of Computer Science and Technology, Hangzhou Dianzi University, Hangzhou, China
Li Zhuang,Cloud Technology Research Center,Department of Computer Science and Technology, Hangzhou Dianzi University, Hangzhou, China
Xiao-Fei Zhang,Department of Computer Science and Engineering, Hong Kong University of Science and Technology, Hong Kong
Xiang-Hua Xu,Department of Computer Science and Technology, Hangzhou Dianzi University, Hangzhou, China
Jian Wan,Department of Computer Science and Technology, Hangzhou Dianzi University, Hangzhou, China
Ivan Simecek,Department of Computer Science, School of Electrical Engineering, Czech Technical University, Czech Republic

Contact